単振り子の話 桂田祐史 07年10月8日, 12/3/2, 訂正 趣味色が強い。情報処理教室で再現してもらうためには、Mathematica でやるのがよいか?単振り子 : 運動方程式 (equation of motion) 鉛直面内で回転運動できるように点 O で固定した軽い棒の先端に質量 m m の質点を取り付けた単振り子について,点 O から引いた鉛直軸 OC と棒とのなす角を θ θ とする(反時計回りに回転する角の向きを正にとる電子情報工学実験I「Mathematicaによる計算処理」において課題と して、アニメーションをだしております。提出された中で良くでき ているアニメーションの例を示します。Mathematicaを動かせる環 境にある人は是非楽しんで下さい。
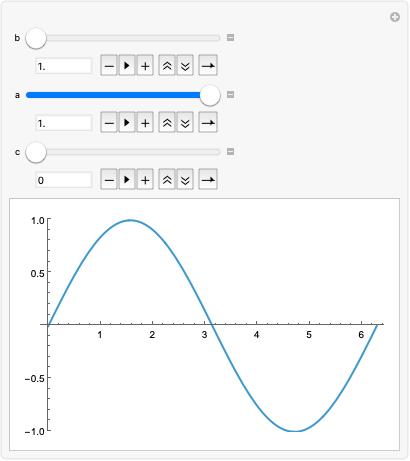
アニメーションを作成する方法 Wolfram言語ドキュメント
Mathematica アニメーション 振り子
Mathematica アニメーション 振り子-52 単振り子 の方程式 Next 53 数値解法の詳細については、そのうち学ぶ機会があると思われるが、 ここでは Mathematica にやらせてみよう。 これまでと同様に DSolveMathematicaによる質点系の力学入門 鉛直上方に投げた質点の運動 運動方程式と境界条件 初速度v = 50 で投げ出す。最初の位置をx = 0 とする。 微分方程式を解いてグラフを描く. アニメーションを表示する. 水平方向に投げた質点の運動 運動方程式と境界条件




数式処理ソフトmathematicaで数学の問題を解く
Mathematica による高校物理シミュレーション 日本女子大学附属高等学校 平井俊成 thirai@fcjwuacjp 1.はじめに 日本女子大学附属高等学校では高校3 年生が自由に選択できる講座を多数用意している。概 要: 本問は,結局は2物体間の 相対運動 の問題に帰着します。 空気抵抗などが無視できるなら,放たれた鉄砲の弾丸も木から飛び出したお猿さんも重力だけを受けて運動しているので,一方から他方(猿から鉄砲の弾丸)を見たときの相対運動では 重力加速度の効果は相殺されてしまいカオスや非線形力学は社会学、経済学、生物学などの分野で広く応用されています。 その中で最もホットな分野の一つは脳科学ではないでしょうか。 脳の振舞いを理解するための研究の一端をシミュレータで紹介します。 Windows、Mac、LinuxなどJavaが動くPC
参考までに、Animateを使ったアニメーション作りの注意点を ここに (Mathematicaファイル ) まとめます。 研究室で役に立つMathematica 学生さんにとってMathematicaは難しいかもしれませんが、ここで学んでおくとこれからの実験や4年生の卒業研究、そして研究室でMathematicaによる簡単な力学 上記の質点の運動を,0 < t < についてアニメーションとして表示してみよ. 7.単振り子 質量mのおもり (質点) が長さlの糸でつり下げられている.この状態から,おもりを水平方向に引 単振り子の運動と位相の同時アニメーション 半径Lの円弧上を質量mの質点が往復運動する振り子について考える。このときの質点の運動方程式は、 $$ mL \frac{d^2 \theta}{dt^2} = mg \sin{\theta} $$ となる。
Mathematica を使ってみよう アニメーションを作るためのコマンドは, Animate変数を含んだ描画関数,{変数,変数の最小値,変数の最大値,変数の増分 } です. (例) 半径が0から1まで01づつ増えていく円のアニメーションを作るAnimate expr, { u, u min, Infinity } makes an infinite animation in which the value of u increases forever at a rate of one unit per second Animate expr, { u, Infinity, Infinity } also allows u to decrease forever if the animation is run in reverse Animate generates a Manipulate object containing an Animator 5アニメーションは静的な表示よりも多くの情報を伝えることができる.組込みの Wolfram言語 関数である Animate および ListAnimate は,グラフィックスあるいは Wolframシステム ノートブック内のどのような種類の式からでもアニメーションを即座に構築する方法を提供する.その他にも



長さを変えた15個の振り子を一斉に揺らす実験 配電盤
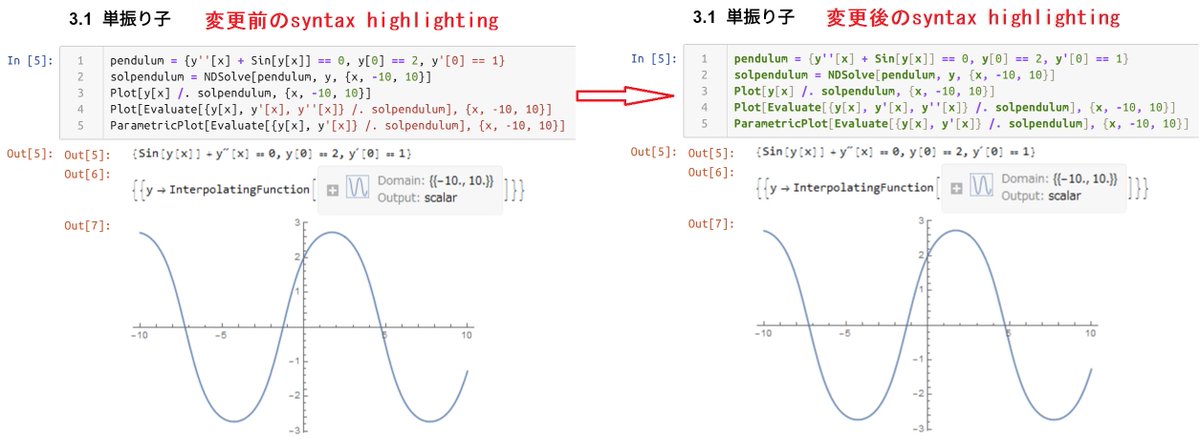



黒木玄 Gen Kuroki Wolframengine Free Wolfram Engine をダウンロードして Jupyter で使えるようにする方法の解説を T Co 2spupdk7ux Free Wolfram Engineをjupyterで使う方法 にまとめておきました T Co Jzrstgsowc
摩擦 , 斜面 , 自由落下 , 放物運動 , 水平投射 , 床・壁面との衝突 円運動 等速円運動 振動 単振動 , 単振り子 , 減衰振動 , 強制振動 , 2体連成振動 その他の運動 粘性抵抗を伴う放物運動 , 2体の万有引力 ホーム >>シミュレーションK:粘性減衰係数 mlθ klθ mgsinθ=0 θ = dθ dt,θ =d 2θ dt2 4 θ(* 例3 バネの運動 その1 *) 図のように質量mの小物体aがx軸上にあり、バネ定数k、自然長lの軽いバネで壁に結びつけられて静止している。



2



Macintosh Hd Desktop Folder 5harmanimation Html
ループを使用したアニメーション for ループ(あるいは while ループ)を 用いることで、簡単にアニメーションを作成することができます。 各ループでそのタイムステップのグラフにアップデートします。 3D アニメーション 例 はじめに イベントに従ってボタンの色を変える、 という単純な実装でハマったので、ここに残します。 animate()の簡単な使い方とともに。 animate()とは DOM上のどんな要素にもstyle属性が指定されていまMathematicaで学ぶシリーズ 3 力学入門 鈴木 真二 東大教授 工博 著;




二重振り子のアニメーションが教えてくれるカオス
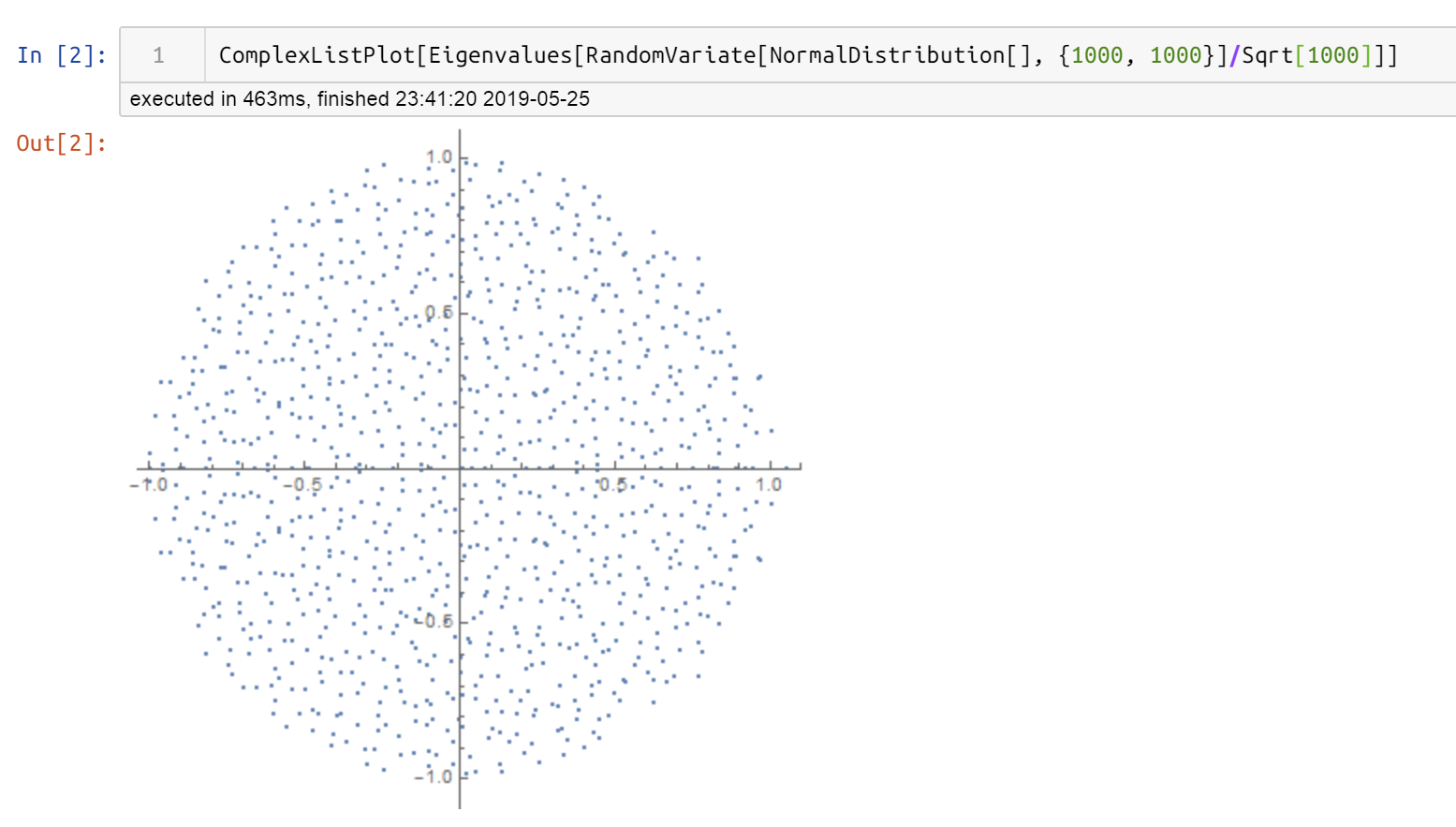



黒木玄 Gen Kuroki Wolframengine Wolfram Engine を Jupyter Notebook で使うときの注意 や のようなユニコード文字を使用せずに Infinity や Gt を使うようにする これ結構大事 何度かはまりました Twitter
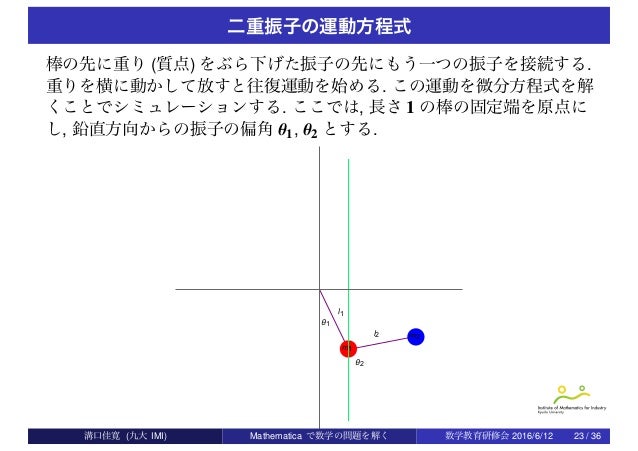
V アニメーション 3 モデル定義 今回は例として単振り子のシミュレーションを行う。 モデル図を以下に示す。 振り子の長さを , 質点の質量を , 振り子の角度を , 重力加速度を とする。 4 運動方程式導出コード1: 運動する点のアニメーションを作成するMATLABスクリプト まず (1)で、点の運動データを作成します。 次に (2)で、Figureに初期の点を plot コマンドで描画し、描画された chart line オブジェクトのハンドルを変数 h に取得しておきます。 最後に (3)のMathematica アニメーション(作成法付き) 微分方程式と曲線群(Differential Equations and Families of curves;Mathematica 6) 振幅の大きな振り子(Pendulum with a large amplitude)
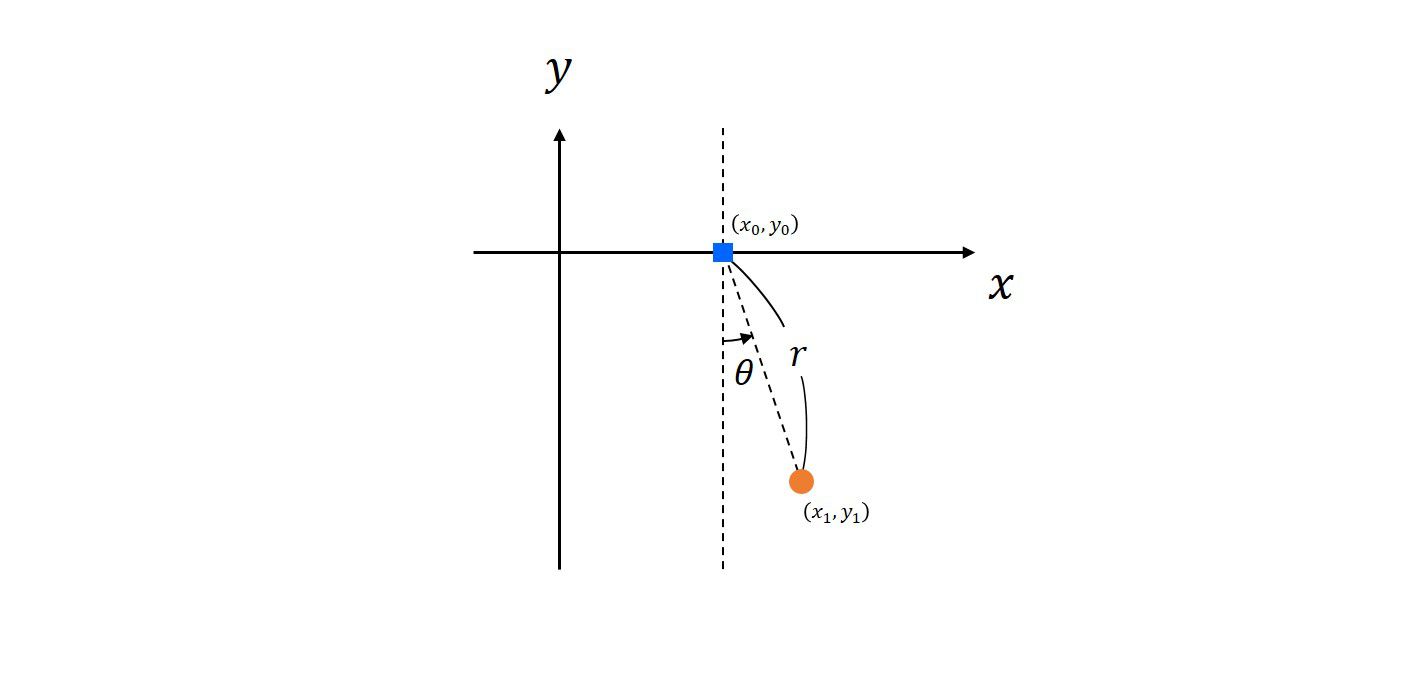



Lagrange シキノート



Macintosh Hd Desktop Folder 5harmanimation Html
Chaos and the Double Pendulum A chaotic system is one in which infinitesimal differences in the starting conditions lead to drastically different results as the system evolves Summarized by mathematician Edward Lorenz, "Chaos is when the present determines the future, but the approximate present does not approximately determine the future" There's an空気抵抗のもとでの放物運動 Timestamp " Fri 0800 JST hig" (いろいろな値の比例定数で)速さの1乗に比例する大きさの空気抵抗の場合です12 アニメーションのための電気力線の描画法 ある時間の電気力線の描き方と、アニメーションのために、ある時間の電気力線がどのよ うに動くかを調べる理論は2に詳しく書かれている。 2次元グラフィックを描く作業を簡単に説明すると、 1



電子情報工学実験i Mathematicaによる計算処理 アニメーション
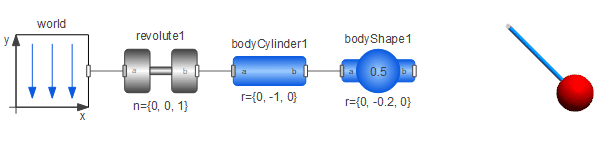



Modelicaの諸相とモデリングについての助言
アニメーションを作成しなさい。ただし、質点 の座標は次式で与えられるものとする。 {x,y}={Cost/t, Sint/t} – {1< t 長さを変えた15個の振り子を一斉に揺らす実験(動画) をMathematicaでシミュレートする。 手順は以下のとおり。 ラグランジの運動方程式は次のように確認できる。 これを使って、シミュレーションを作る。 (* 1分間の振動数が整数になる長さを求める Mathematicaサンプルコード シミュレーションサンプルコードを共有しておきます。 初めての場合は単振子から始めて下さい。 単振子についてはドキュメントも併せておいておくので各自読みながら勉強してみて下さい。 二重振子・倒立振子も作ってみたの




Mathematicaを用いて振り子の支点が移動 ひもの長さが変化 するとき 物理学 教えて Goo



Mathematica Lecture Notes Nwada Home No2
Mathematicaでアニメーション 概要 一枚一枚の画像をまとめて Table に納め, それを望みの形式( mov,gif,avi など)で Export すれば良い. 手順 時刻 t の画像1枚を描く関数を定義する 例:密度プロットを行う Mesh > False 又は True オプションとして、xy方向にメッシュを描くかどうか定める AspectRatio > Automatic オプションとして、図の縦横比を指定する Animate Plot (3D) f, {x, nmin, nmax}, {y, nmin, nmax}, {n, min, max, step} アニメーション表示 ContourPlot fMathematica をプログラミング言語と考えたときの文法と,関数電卓と同 じような計算をさせるにはどのようにすれば良いのか,という基本的なこ とを学びます。この章の到達目標は,次のような計算を Mathematica にさ せることになります。



専修大学ネットワーク情報学部プロジェクト発表会09 プロジェクト紹介



電子情報工学実験i Mathematicaによる計算処理 アニメーション
Mathematica で微分方程式を解くには DSolve を使います。 Mathematica に限らずアプリケーションは、いろいろ試しながら 覚えるのが上達の早道ですから、さっそく次のように入力してみましょう。 *以降このフォントは Mathematica の入力の意味に使います。Mathematicaでのファイル保存を「HTML形式」保存(GIFファイルができます) GIFアニメ作成ツールで作成(Animation GIF Maker) y=sin(x a) ( a=04 2 )のグラフ 作成手順(その2)4 第1章 Matlab入門1 2 1 X= 21 4 67 5 Y= 03 2 23 7 86 8 演習 1 A,B を入力して,AB を計算するプログラムを作成せよ.そして,つぎの場合 を計算してみよ. (1) A = 1111, B = 1 2 3 4




アイデア実現のための Raspberry Piデザインパターン 電子回路からmathematicaによるarduinoコラボまで 理工学専門書 電子 電子一般 Ohmsha
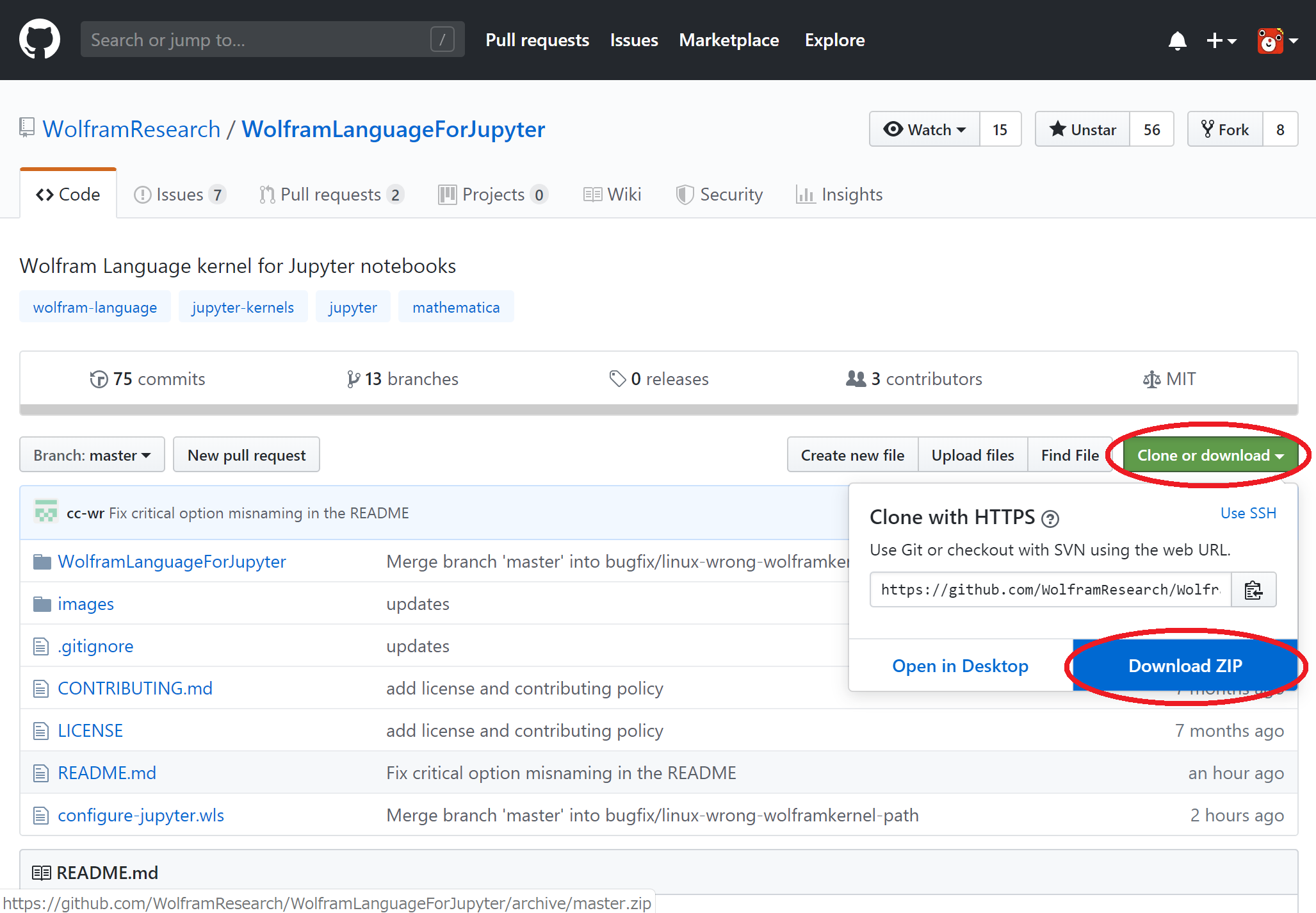



O Xrhsths 黒木玄 Gen Kuroki Sto Twitter Wolframengine Wolfram Engine Mathematica と Sympy を比較すると数式処理の能力ではwolfram Engine の方が圧倒的に勝っているという印象があります 誰か Julia言語 から Wolfram Engine を Sympy なみに使えるように
M質量 θ:角度 t:経過時間 g:重力加速度(98)!アニメーション 次を実行すると,n 0, ,9 の10 枚のグラフィックが得られる.見れば分かると思うが,サインカーブをx 軸方向に少しずつ平行移動したものである. Table Plot Sin x nPi/5 ,アニメーション In 24= Out 24= β < の時は軌跡は螺旋を描き原点に収束する. β ≥ 0 の場合は螺旋は描かず直接原点に収束する.この収束した点を 固定点 (fixed point) またはポイントアトラクター (point attractor) と呼ぶ.このケースでは ポイント



電子情報工学実験i Mathematicaによる計算処理 アニメーション



Mathematica Lecture Notes Nwada Home No2
Raspberry Pi上で無料で使えるMathematica (マセマティカ)を使ってみます。 Raspbianをインストールしていれば、Mathematicaもインストールされていますので、マウス操作で左上のアプリケーションメニューからMathematicaを起動します。 ロゴが出てしばらく待つとMathematicaが用意している数学関数は、はじめが大文字であることに注意。 Sqrt16 16の平方根の計算 Prime15 15番目の素数を求める FactorInteger01 素因数分解 Helpの使い方 Mathematicaには無数の数学的関数が組み込んであり、すべてを覚えるのは不可能である



Mathematicaの課題でモンキーハンティングのアニメー Yahoo 知恵袋




振子の周期的揺れの動きのシミュレーション Matlab Simulink Example Mathworks 日本



長さを変えた15個の振り子を一斉に揺らす実験 配電盤



電子情報工学実験i Mathematicaによる計算処理 アニメーション



Macintosh Hd Desktop Folder 5harmanimation Html



電子情報工学実験i Mathematicaによる計算処理 アニメーション




らくらく Dcl 辻野 智紀 神戸大学 理学部 地球惑星科学科 B4 Ppt Download
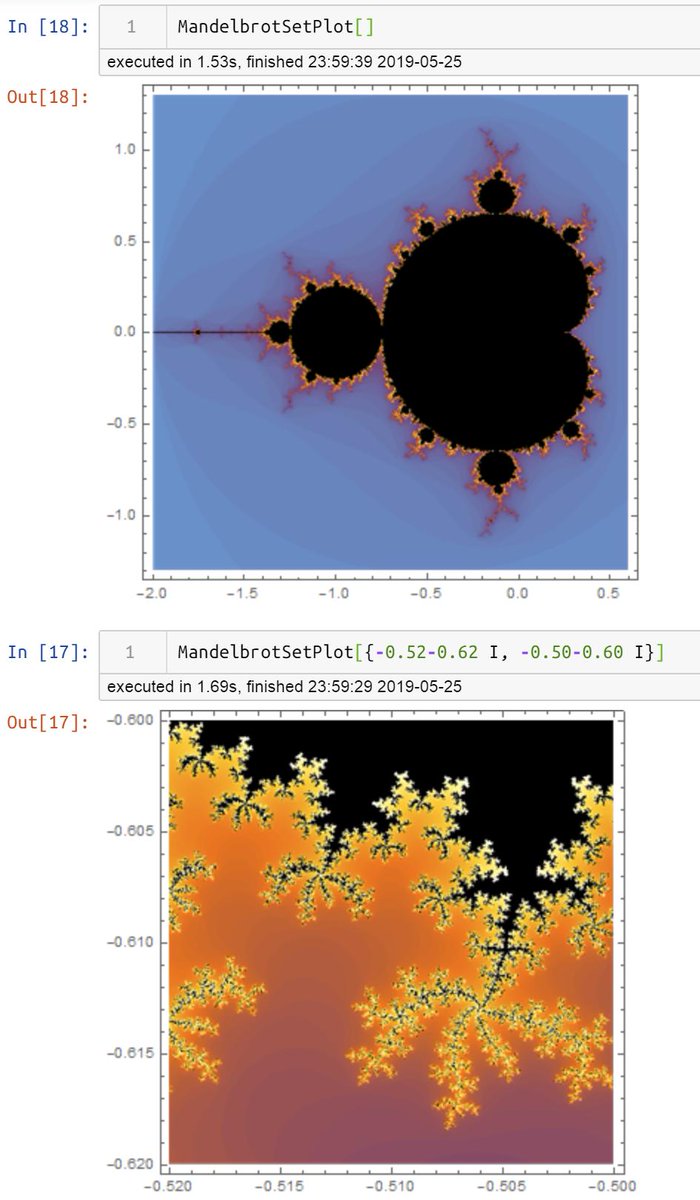



黒木玄 Gen Kuroki Wolframengine 無料でダウンロードしたwolfram Engineで振り子の微分方程式を解いた見た



電子情報工学実験i Mathematicaによる計算処理 アニメーション



電子情報工学実験i Mathematicaによる計算処理 アニメーション
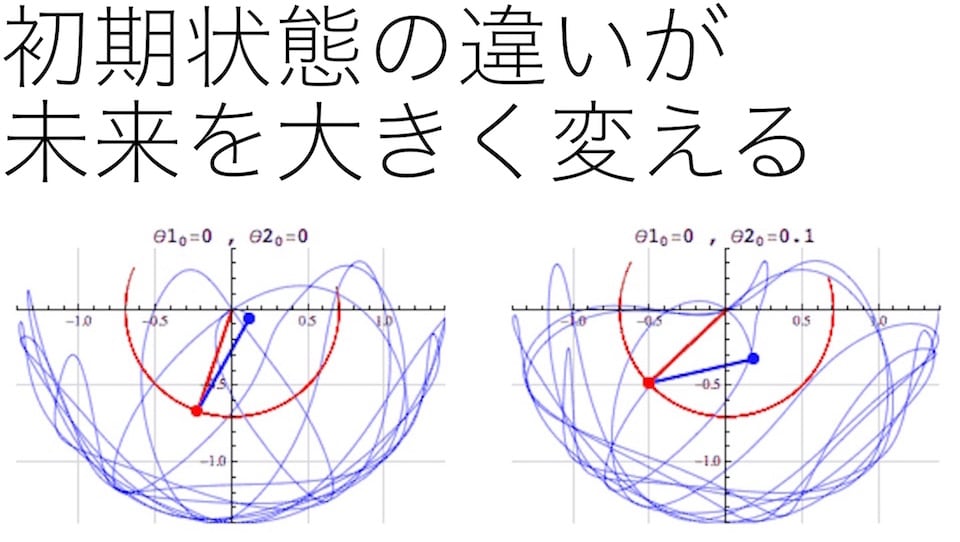



二重振り子のアニメーションが教えてくれるカオス
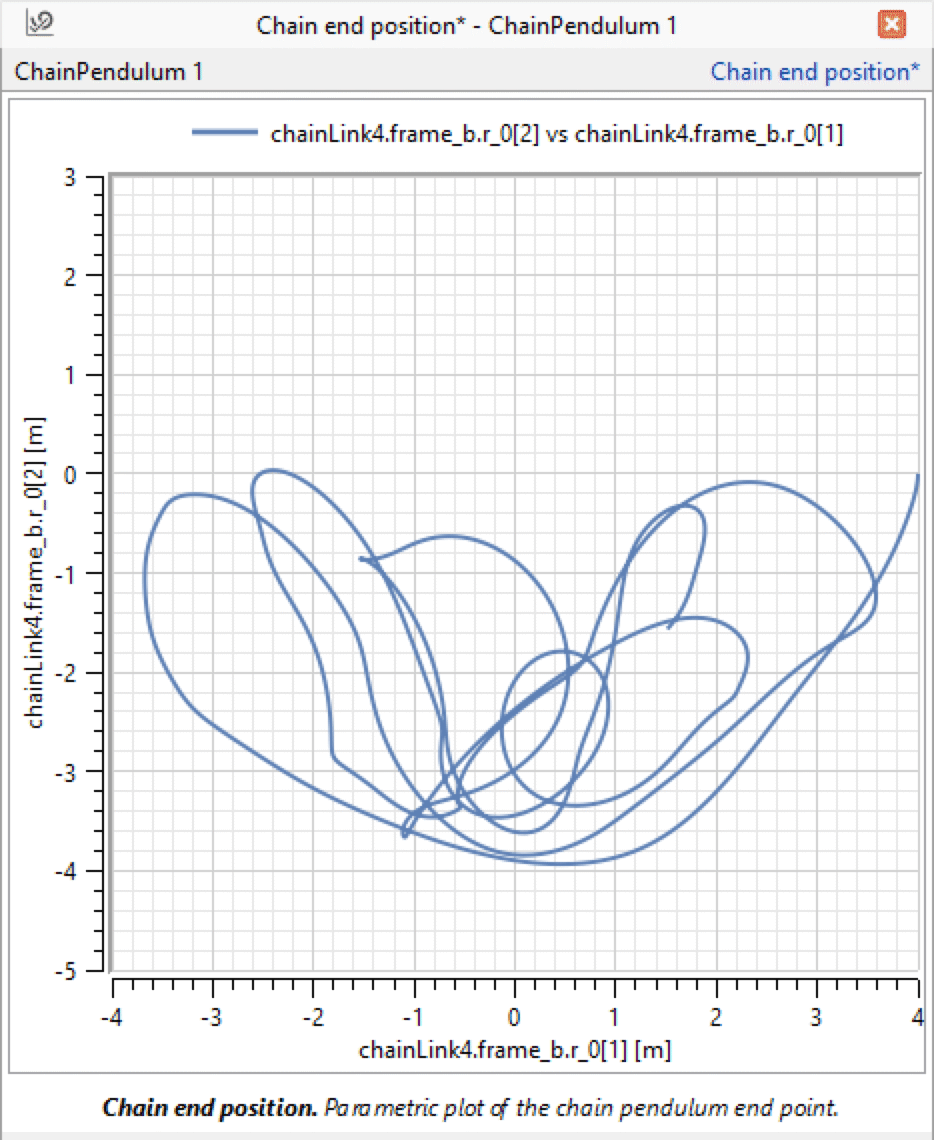



カスタムコンポーネント チェーン振り子




アニメーションを作成する方法 Wolfram言語ドキュメント



Macintosh Hd Desktop Folder 5harmanimation Html




アニメーションを作成する方法 Wolfram言語ドキュメント
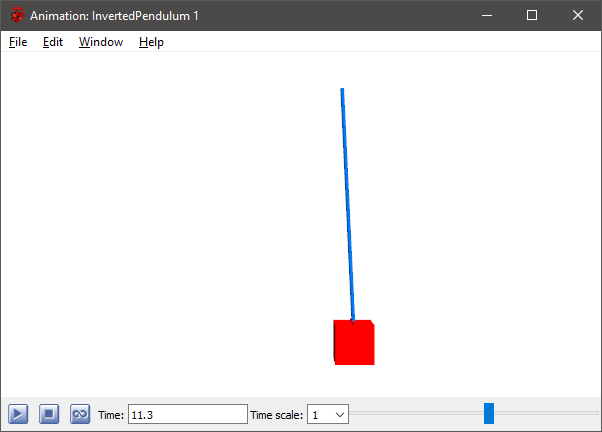



系 倒立振り子
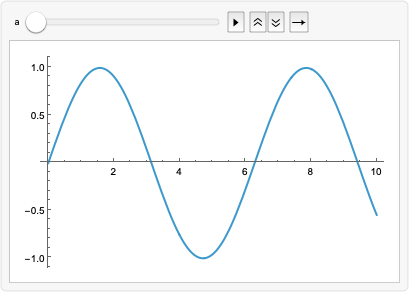



Animate Wolfram言語ドキュメント
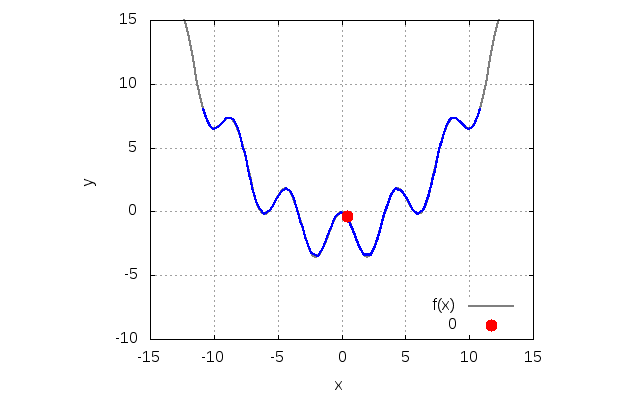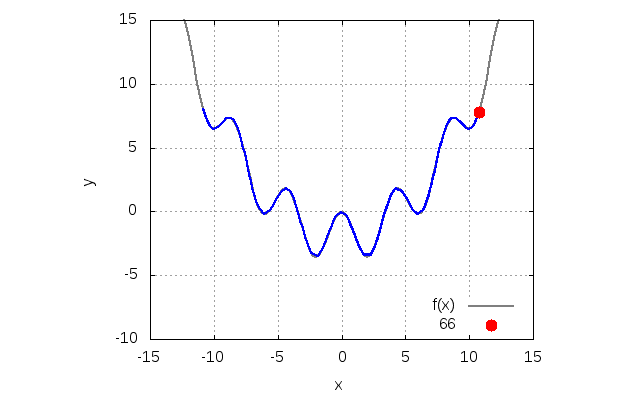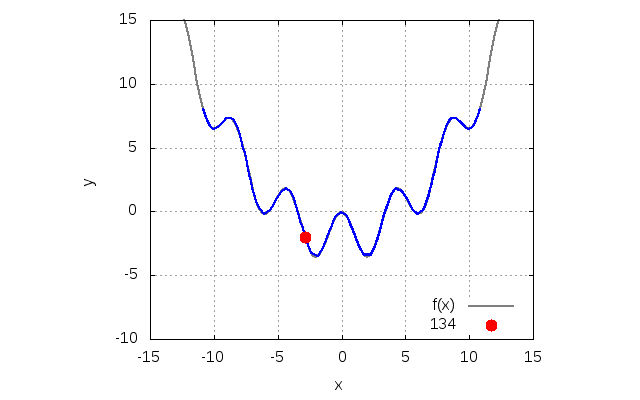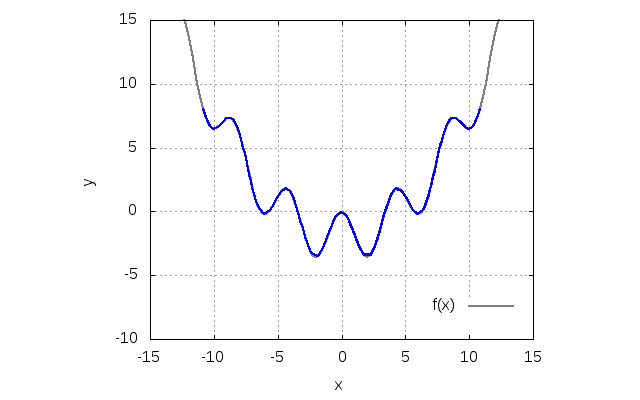



Lagrange シキノート



Eac8u4xj0g4yem



Physicsisfun05 Nb



Scilabによる単振り子のアニメーション 制御系cad
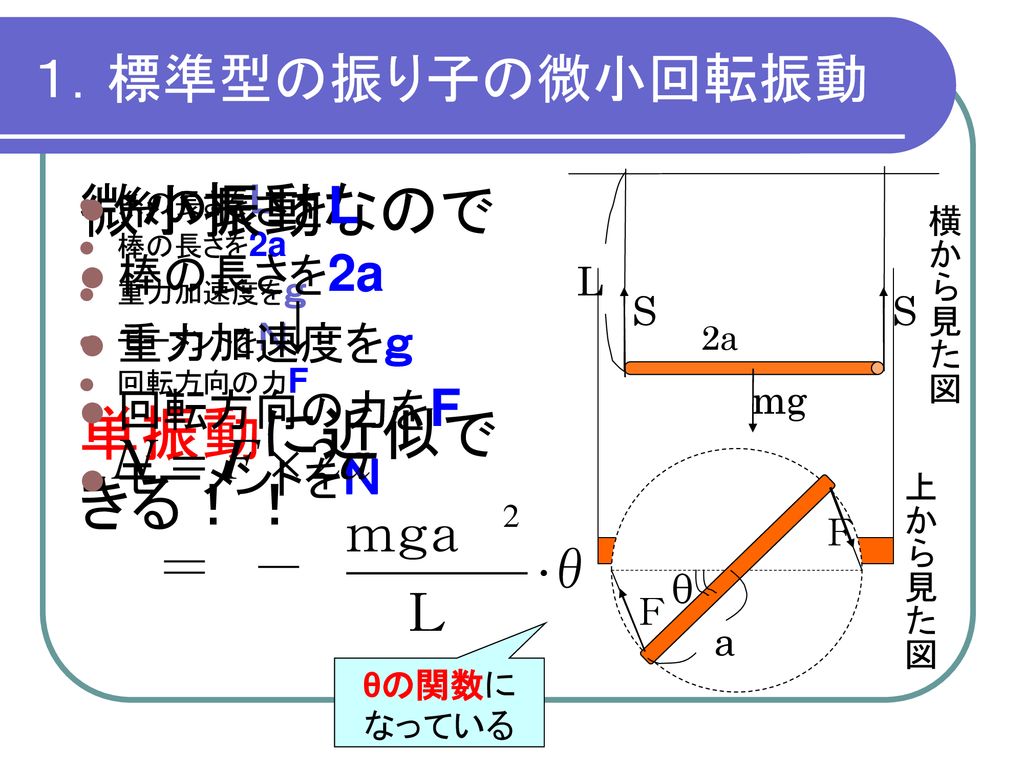



メンバー 梶川知宏 加藤直人 ロッケンバッハ怜 指導教員 藤田俊明 Ppt Download




ロボット工学 第12回 解析力学の基礎 福岡工業大学 工学部 知能機械工学科 木野 仁 Ppt Download



電子情報工学実験i Mathematicaによる計算処理 アニメーション
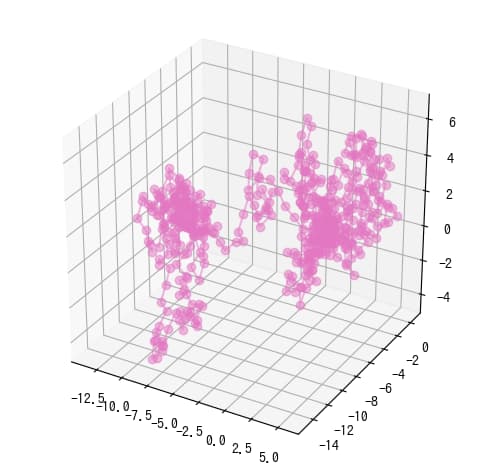



Matplotlib Animation 66 3次元ランダムウォークアニメーション サボテンパイソン
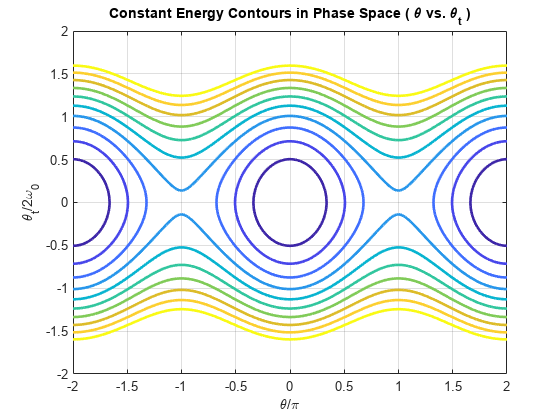



振子の周期的揺れの動きのシミュレーション Matlab Simulink Example Mathworks 日本



電子情報工学実験i Mathematicaによる計算処理 アニメーション




人気の たこルカの物理 動画 47本 ニコニコ動画
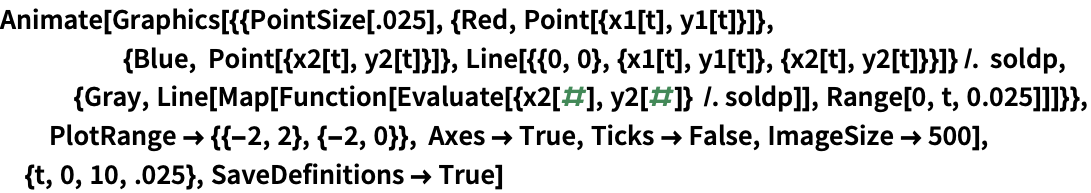



二重振子



Physicsisfun05 Nb



Http Www Math Twcu Ac Jp Ogita Lec Sim Furiko Pdf



Scilabによる単振り子のアニメーション 制御系cad




数式処理ソフトmathematicaで数学の問題を解く



Macintosh Hd Desktop Folder 5harmanimation Html



Mathematica Lecture Notes Nwada Home No2



電子情報工学実験i Mathematicaによる計算処理 アニメーション



Mathematica Lecture Notes Nwada Home No2



Physicsisfun05 Nb




振子の周期的揺れの動きのシミュレーション Matlab Simulink Example Mathworks 日本



Http Www Math Twcu Ac Jp Ogita Lec Sim Furiko Pdf




二重振り子のアニメーションが教えてくれるカオス



長さを変えた15個の振り子を一斉に揺らす実験 配電盤



ニュートンのゆりかごの原理は何ですか Yahoo 知恵袋
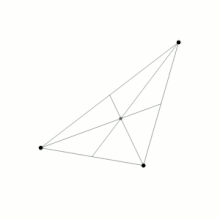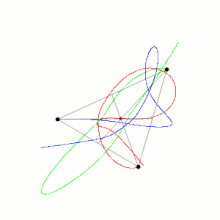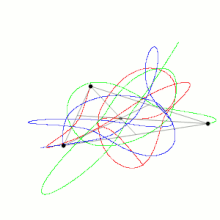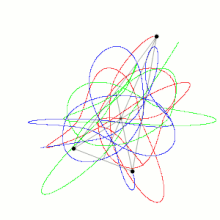



三体問題 Wikipedia



Scilabによる単振り子のアニメーション 制御系cad



電子情報工学実験i Mathematicaによる計算処理 アニメーション



電子情報工学実験i Mathematicaによる計算処理 アニメーション



電子情報工学実験i Mathematicaによる計算処理 アニメーション



Macintosh Hd Desktop Folder 5harmanimation Html
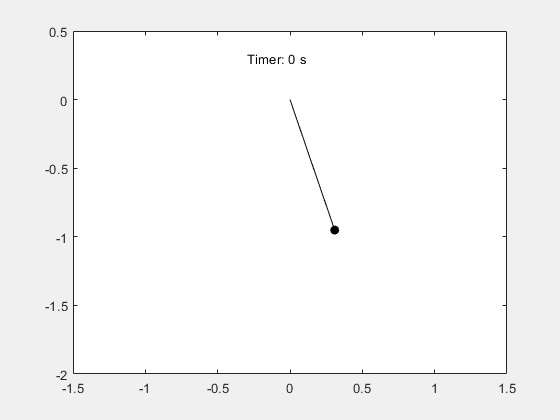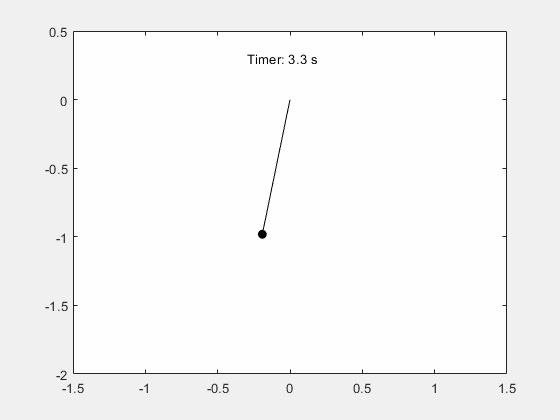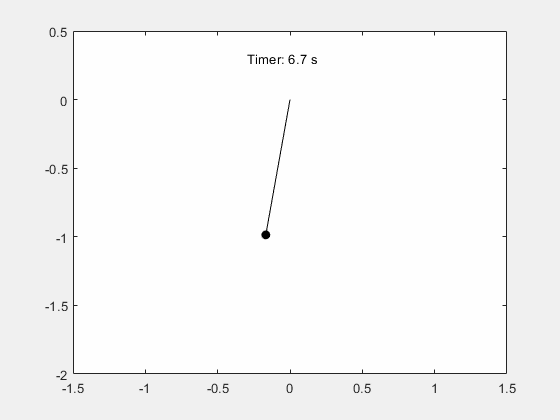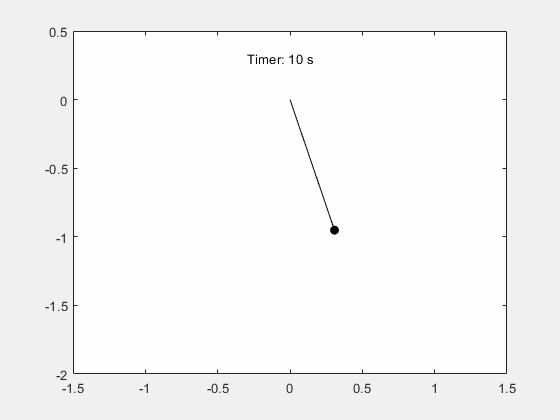



振子の周期的揺れの動きのシミュレーション Matlab Simulink Example Mathworks 日本



Doublependulumdemo




Oscillation Wikipedia The Free Encyclopedia Com Imagens Engenharia Mecanica Fisica Engenharia
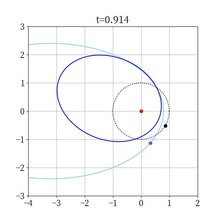



天体力学 Wikipedia



2




Javascriptの三角関数とcanvasで円運動アニメーションを作る



Doublependulumdemo
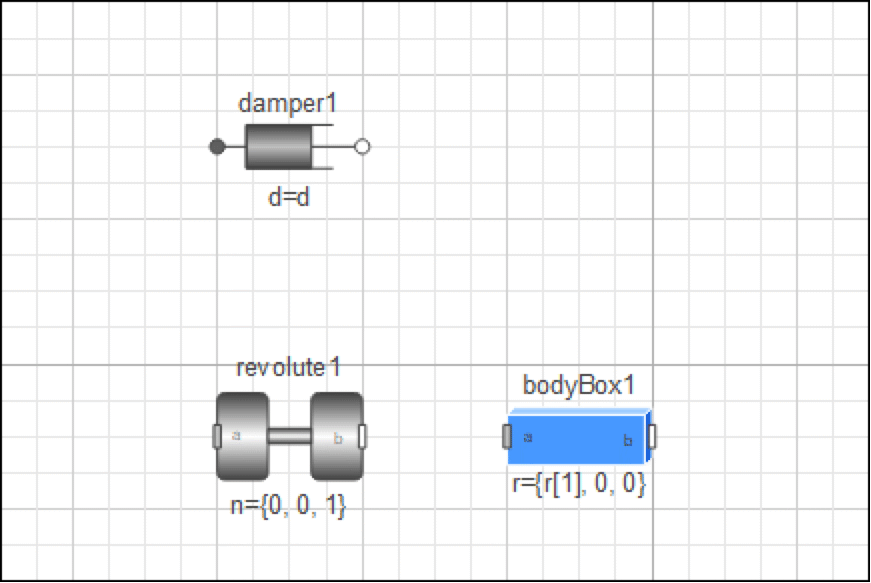



カスタムコンポーネント チェーン振り子



二重振り子のアニメーションが教えてくれるカオス



電子情報工学実験i Mathematicaによる計算処理 アニメーション




天体力学 Wikipedia



電子情報工学実験i Mathematicaによる計算処理 アニメーション



スラックラインの数理 1 ピッチブレンド Blog
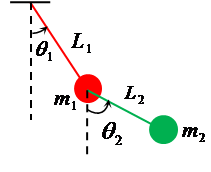



二重振子運動のアニメーションと解 Matlab Simulink Example Mathworks 日本



電子情報工学実験i Mathematicaによる計算処理 アニメーション



電子情報工学実験i Mathematicaによる計算処理 アニメーション



Doublependulumdemo
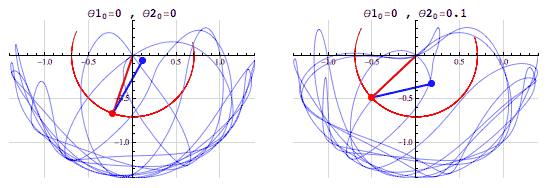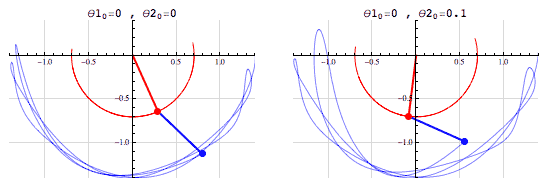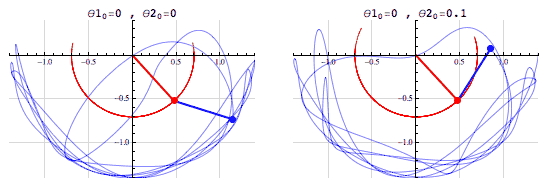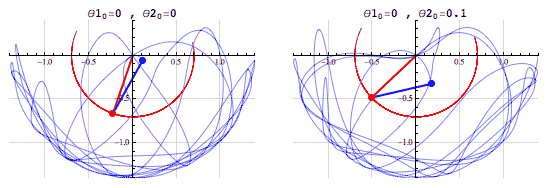



二重振り子のアニメーションが教えてくれるカオス
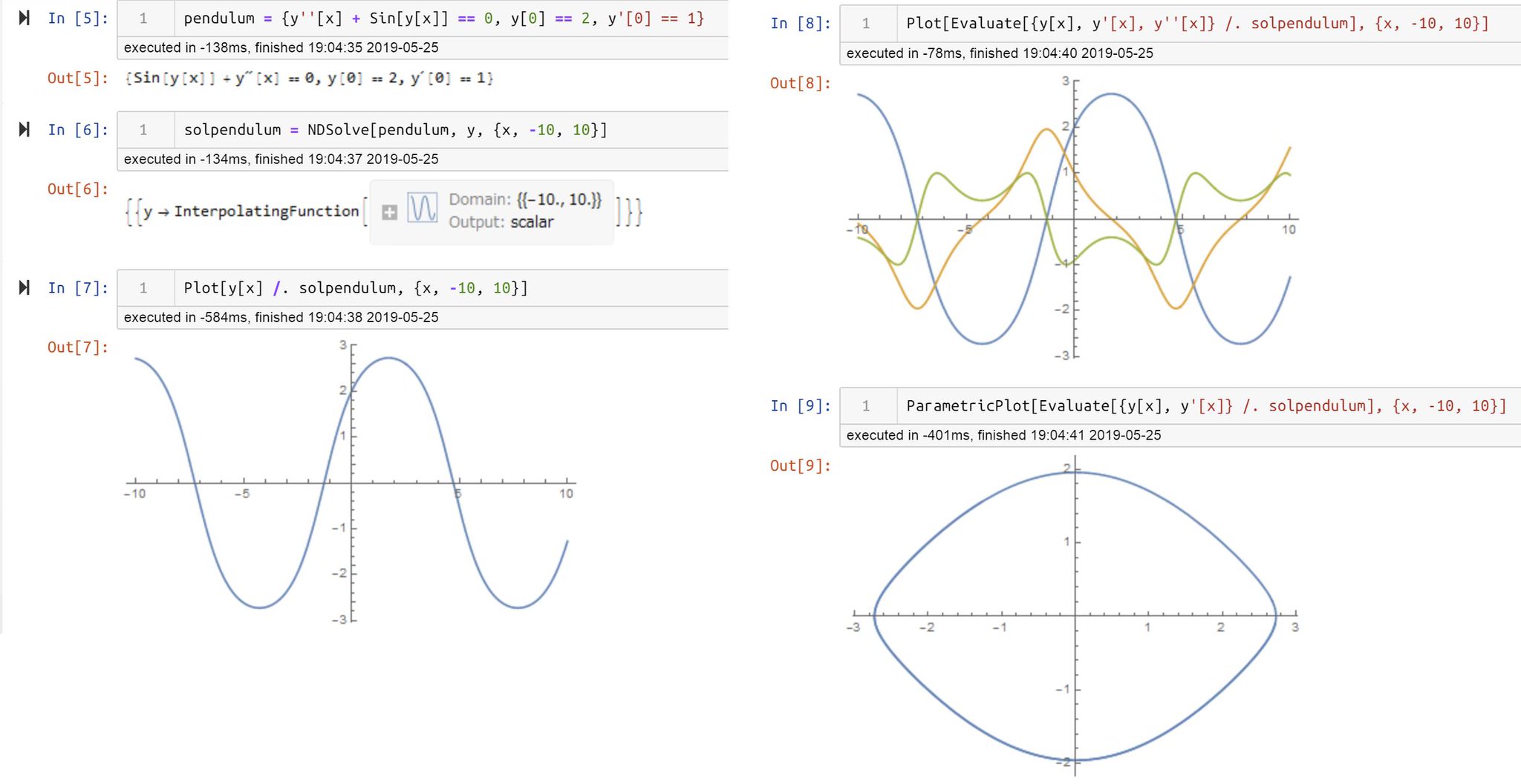



黒木玄 Gen Kuroki Wolframengine 無料でダウンロードしたwolfram Engineで振り子の微分方程式を解いた見た
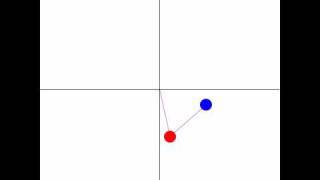



溝口 佳寛 Yoshihiro Mizoguchi 研究ノート Researchmap




レゴのセグウェイ 倒立振り子の制御 Systemmodelerのモデル
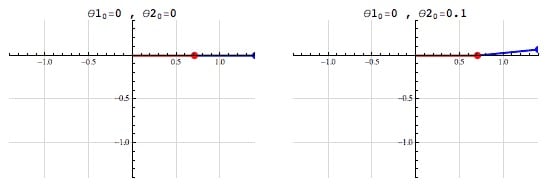



二重振り子のアニメーションが教えてくれるカオス




溝口 佳寛 Yoshihiro Mizoguchi 研究ノート Researchmap
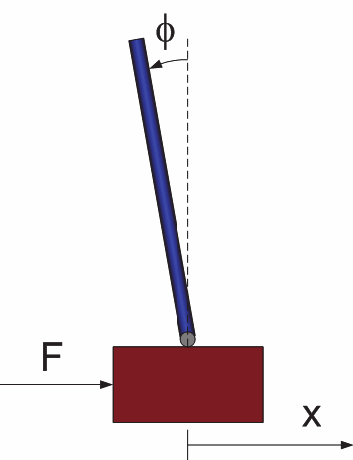



系 倒立振り子



Macintosh Hd Desktop Folder 5harmanimation Html




物理エンジン 4重振り子で突然やって来るカオス現象 Youtube




メンバー 梶川知宏 加藤直人 ロッケンバッハ怜 指導教員 藤田俊明 Ppt Download




Mathematicaブック スティーブン ウルフラム Nsulpokicirc
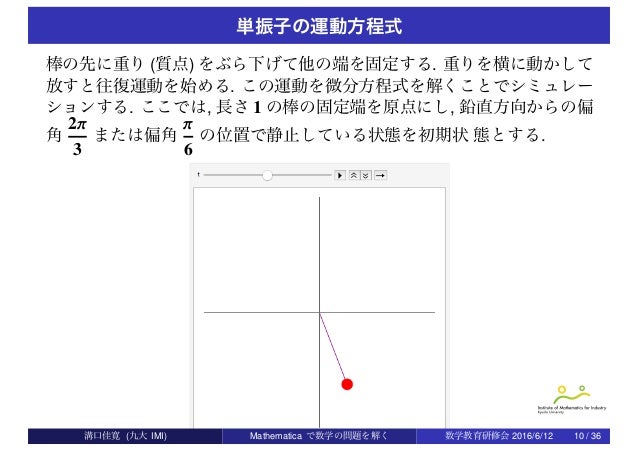



マセマティカ
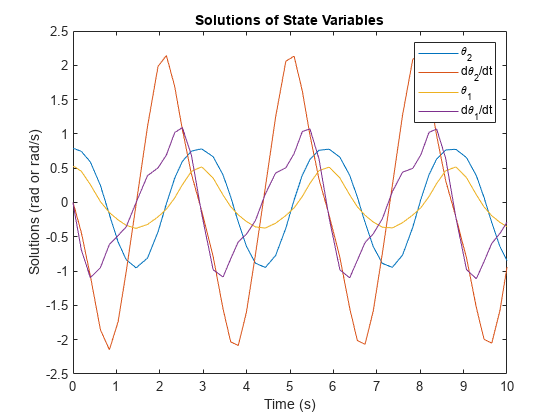



二重振子運動のアニメーションと解 Matlab Simulink Example Mathworks 日本



Pov Rayによる数学お絵かき入門 Advent Calendar 17 Qiita



電子情報工学実験i Mathematicaによる計算処理 アニメーション
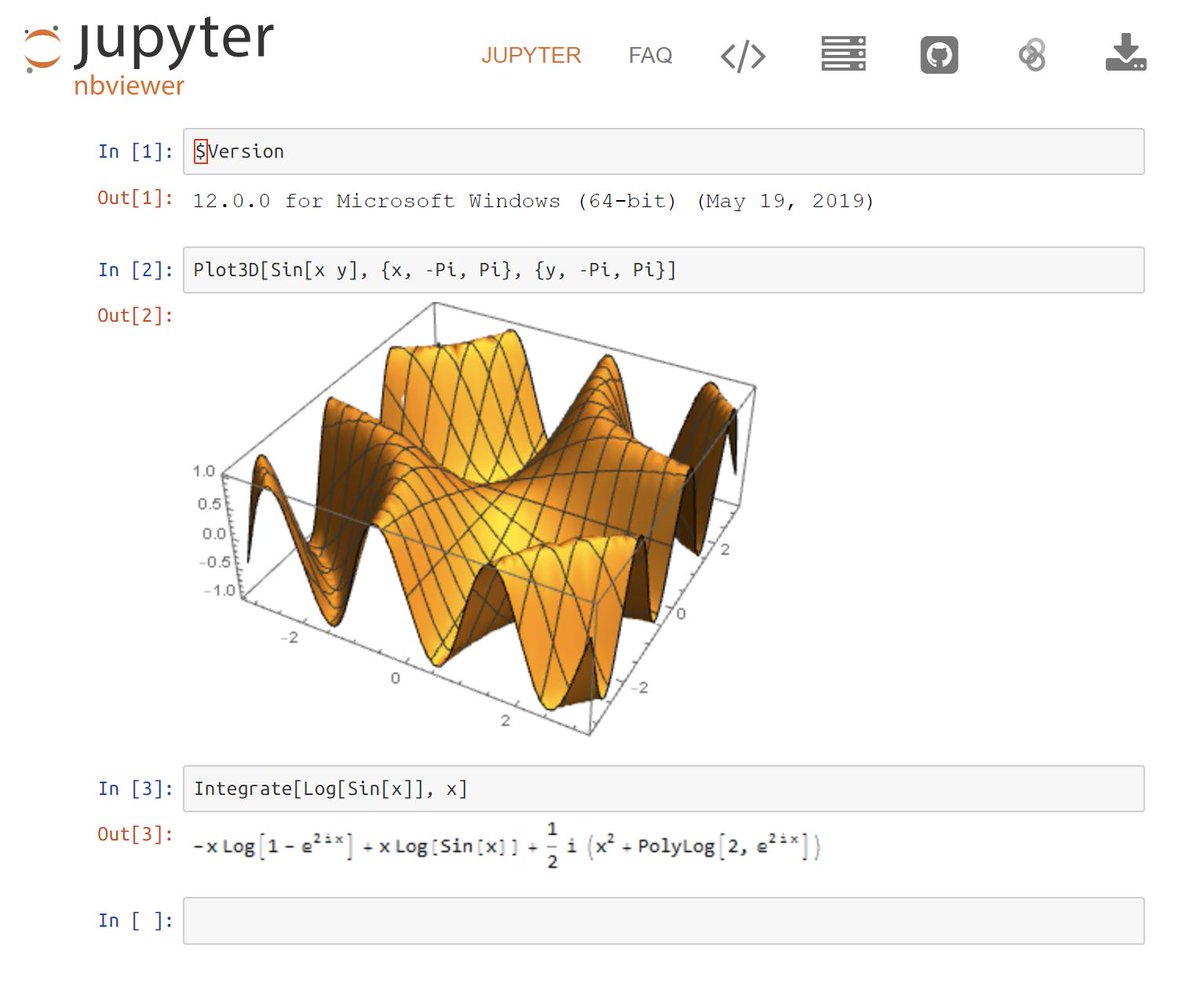



黒木玄 Gen Kuroki Wolframengine 無料でダウンロードしたwolfram Engineで振り子の微分方程式を解いた見た



0 件のコメント:
コメントを投稿